Ak vzorka sa nachádza mimo magnetického poľa (B0 = 0) potenciálna energia (EΘφ= -μz.B0 ) všetkých spinov, nezávisle od ich orientácie je rovnaká – nulová. Z Boltzmanovho zákona potom vyplýva, že všetky orientácie spinov v priestore sú rovnako zastúpené. Pri nulovom poli je aj frekvencia precesie (ω0=γ.B0) nulová. Mimo magnetického poľa sú teda spiny statické objekty, ktoré si zachovávajúce svoju orientáciu v priestore. Ak by sme počiatky vektorov magnetického momentu jednotlivých spinov presunuli do počiatku súradnicovej sústavy potom by konce vektorov boli vytvárali povrch (Blochovej) gule, pričom hustota koncov vektorov vo všetkých orientáciách by bola rovnaká. Situácia je symbolicky znázornená na nasledujúcom obrázku.
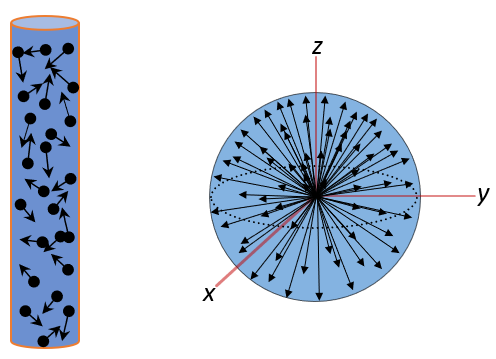
Keďže všetky orientácie sú rovnako pravdepodobné, ku každému magnetickému vektoru existuje aj opačne orientovaný vektor, ich súborový súčet (rovnovážna magnetizácia M0) je preto nulový: M0 (B0=0) =∑i μi = 0. Podobne ako celková rovnovážna magnetizácia vzorky aj magnetizácie jej zložiek sú pri nulovom vonkajšom magnetickom poli nulové: M0k(B0=0) =0, pre všetky zložky k.







