Základným mechanizmom relaxácie spinov s I=1/2 sú ich interakcie s náhodnými magnetickými poľami od susedných spinov, elektrónov a paramagnetických látok vo vzorke. Pôsobenie týchto náhodných magnetických polí si možno predstaviť ako sériu krátkych náhodných impulzov na spiny v rôznych lokalitách vzorky.
Medzi najdôležitejšie náhodné polia generované v rámci molekuly patria polia vybudené interakciou Bo s elektrónovým oblakom molekuly (tieto polia súvisia s tzv. chemickým posunom spinov) a polia súvisiace s interakciou medzi dvojicou spinov prenášanou priamo cez priestor (označenie DD interakcie) alebo prenášanou nepriamo cez väzby prostredníctvom väzbových elektrónov (označenie J interakcie). Okrem relaxácie tieto interakcie sú “zodpovedné” aj za vznik a vzhľad NMR spektier a ich podrobnejšia diskusia je uvedená nižšie.
Charakteristika náhodných magnetických polí
Zdrojom pohybu atómov a molekúl generujúcich premenlivé magnetické polia je tepelný pohyb vo vzorke. Ten je ovplyvnený skupenským stavom vzorky, jej teplotou a viskozitou ako aj veľkosťou a tvarom molekúl. Je to náhodný chaotický pohyb, ktorého časový priebeh je ilustrovaný na obrázku 13 v jeho hornej časti.
Matematicky sa náhodný pohyb charakterizuje pomocou tzv. autokorelačnej funkcie G(t,τ). Je to funkcia času (zvaná tiež pamäťová funkcia), ktorá porovnáva stav nejakej vlastnosti systému v počiatočnom čase t so stavom tej istej vlastnosti v čase t+τ. Ako príklad vlastnosti systému uvažujme hodnotu magnetického poľa medzi dvojicou spinov I a S nachádzajúcich sa v tej istej molekule. Veľkosť a orientácia vektora ktorým spin S pôsobí na spin I budú vo všeobecnosti pre každú molekulu iné a budú sa s časom pri pohybe molekúl meniť. Označme vektor magnetického poľa, ktorým spin S pôsobí na spin I v i-tej molekule v čase t ako Bi(t) a v čase t+τ ako Bi(t+τ) a urobme ich vektorový súčin Bi(t).B*i(t+τ). Následne urobme rovnaký vektorový súčin vo všetkých molekulách vzorky. Pamäťovú funkciu G(t,τ) potom možno vyjadriť ako súborové spriemernenie tohto súčinu: G(t,τ) = 1/NΣiBi(t).B*i(t+τ), kde N je počet molekúl vo vzorke. Pre stacionárny náhodný proces (náhodný proces, ktorého charakter sa s časom nemení) autokorelačná funkcia nie je závislá od počiatku merania času t ale iba od dĺžky intervalu τ. Pre taký proces platí G(τ)=1/N Σi Bi(0).B*i(τ).
Uvažujme aký bude časový vývoj funkcie G(τ). V čase τ =0 sú vo všetkých molekulách vektory Bi(0) a B*i(τ=0) totožné a teda ich súčin bude kladný a maximálne veľký: Bi(0).B*i(τ) ≧ 0. G(0) je teda tvorená iba súčtom kladných čísiel (súčet štvorcov veľkosti vektorov) a preto G(0) bude mať maximálnu kladnú hodnotu.
Po veľmi krátkom intervale τ možno predpokladať, že veľkosť i orientácia vektora Bi(τ) budú zmenené iba veľmi málo. Zmeny veľkosti Bi(τ) spôsobené zmenou vzdialenosti medzi spinmi I a S môžu byť vo veľkom súbore molekúl kladné i záporné a ich vplyv na zmenu hodnoty autokorelačnej funkcie bude do značnej miery kompenzovaný a možno ho v prvom priblížení zanedbať. Na druhej strane zmena orientácie Bi(τ) jednoznačne zmenšuje hodnotu skalárneho súčinu vektorov Bi(0) a B*i(τ) čo sa prejaví na zmenšení hodnoty G(τ). Postupom času sa orientácia vektorov Bi(0) a B*i(τ) bude z pôvodne usporiadaného paralelného stavu postupne meniť na štatistický náhodný stav. V súborovom súčte ΣiBi(0).B*i(τ)) budú pribúdať záporné členy a pamäťová funkcia sa bude postupne blížiť k nulovej hodnote G(τ) → 0.
Nulovú hodnotu G(τ), ktorá sa teoreticky dosiahne pri τ →∞ možno považovať za jej rovnovážnu hodnotu. Odchýlku G(τ) od tejto rovnovážnej hodnoty potom podobne ako pri iných termodynamických procesov možno považovať za hnaciu silu jej časového vývoja. Dostaneme sa takto k exponenciálnemu vyjadreniu časovej závislosti pamäťovej funkcie: G(τ) = G(0). exp(-τ /τc), kde konštanta τc charakterizuje rýchlosť zániku pamäťovej funkcie. Konštanta τ c sa nazýva korelačný čas a charakterizuje rýchlosť zániku pamäťovej funkcie. Číselne je τc rovný priemernému času za ktorý hodnota G(τ) poklesne na cca 37% pôvodnej maximálnej hodnoty G(0).
Pretože náhodné procesy prebiehajú rovnakým spôsobom aj pri posune času t do minulosti (do záporných hodnôt) je funkcia G(τ) symetrická okolo počiatku (τ =0). Čo možno zapísať ako
G(τ) = G(0).exp(-|τ |/τc)
pričom τ sa mení od –∞ do +∞. Typický priebeh pamäťovej G(t) funkcie je zobrazený na obrázku 13 v jeho ľavej časti.
Fourierovou transformáciou G(τ) sa získa frekvenčné spektrum (spektrálna funkcia) náhodných pohybov J(ω), ktoré zobrazuje distribúciu náhodných pohybov (závislú od hodnoty τc ) ako funkciu ich frekvencie ω.
G(0).exp(-|τ|/τ c) — FT→ J(ω) = k.(τ c/[1+ (ωτ c) 2]) = k. j(ω)
,kde konštanta k závisí od amplitúdy náhodných polí Bi(t); j(ω)= J(ω)/k= (τc/[1+ (ωτc) 2]) je tzv. redukovaná spektrálna hustota, ktorá súvisí iba s frekvenčnou distribúciou náhodných polí. j(ω) je charakterizovaná korelačným časom τc a vyjadruje hustotu náhodných polí od ich frekvencie. Tvar j(ω) pre 3 vybrané hodnoty τc je ukázaný v pravej časti obrázku 13.
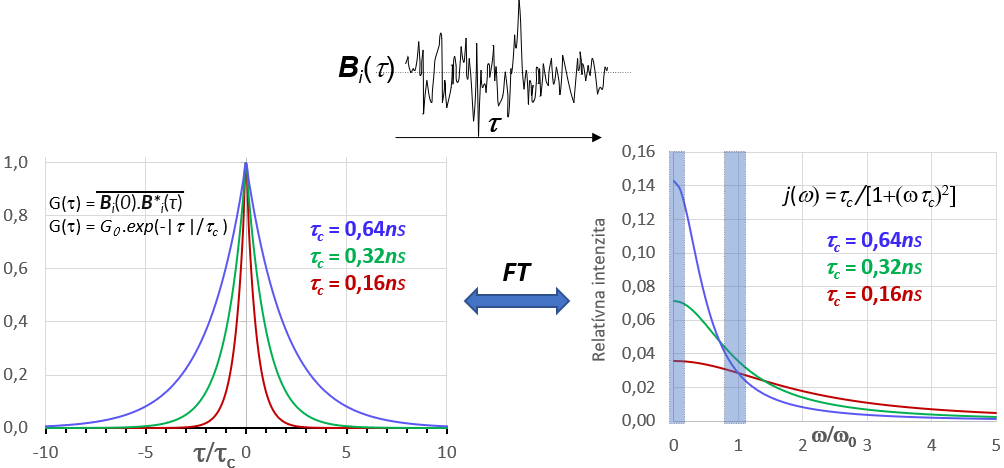
Pre relaxáciu spinov je dôležitá hustota náhodných pohybov iba v určitých špecifických frekvenčných oblastiach. Pre všetky relaxačné mechanizmy (pozri nižšie) sú to vždy 2 frekvenčné oblasti j(ω) na obr.13 vyznačené modrou farbou. Je to oblasť rezonančnej frekvencie spinov (oblasť frekvencie tzv. jednokvantových spektrálnych prechodov) a oblasť v blízkosti nulových frekvencií. Pri relaxačných mechanizmoch spojených so silnou vzájomnou interakciou spinov je dôležitá spektrálna hustota aj oblasti s frekvenciou rovnou frekvencií tzv. viackvantovým spektrálnym prechodom (pozri v ďalšom: dipól-dipólová relaxácia).
Z tvaru spektrálnej funkcie j(ω) je zrejme, že hustota spektrálnych pohybov je vždy väčšia pri nižších frekvenciách. Z toho vyplýva, že hustota pohybov na rezonancií spinov bude väčšia pri spektrometroch z nižšou pracovnou frekvenciou (so slabším magnetickým poľom Bo). Z toho taktiež vyplýva, že relaxácia spinov je pri nižších magnetických polia bude efektívnejšia ako pri vyšších poliach.
Keďže rezonančná frekvencia spinov závisí od indukcie Bo pre vizualizáciu závislosti j(ω) od frekvencie náhodných pohybov je niekedy výhodnejšie ju vyjadriť v relatívnych (bezrozmernej) jednotkách j(ω) = F(ω/ω0). Relatívna stupnica je použitá aj na obrázok 13. Z porovnania závislosti j(ω) pre rôzne hodnoty τc je zrejme, že hustota náhodných polí je najväčšia ak prevrátená hodnota τc je v rezonancií s frekvenciou spinov, t.j. ak 1/τc= ω0 .
To že efektivita relaxácie spinov závisí najmä od hustoty spektrálnych pohybov v oblasti rezonancie spinov (v grafe j(ω) oblasť ω/ω0~1) vyplýva z faktu, že z-zložku magnetizácie Mz možno efektívne zmeniť iba rf. poľom B1 ktorého frekvencia je blízka frekvencií precesie spinov (pozri závislosť účinku B1 od ofsetu). V závislosti od orientácie B1 jeho impulzami môžu meniť orientáciu všetkých zložiek magnetizácie vzorky (Mz↔ My, Mz↔ Mx , Mx↔ My). Náhodné polia Bi(t) s frekvenciou blízkou rezonančnej frekvencií spinov majú v tomto smere rovnaké vlastnosti pole B1. Pretože ich orientácia v priestore je vo všetkých smeroch rovnako pravdepodobná budú rovnakým spôsobom prispievať k zmene a teda aj relaxácií Mz i Mxy. Jediný rozdiel medzi pôsobením B1 a polí Bi(t) je, že B1 počas svojho trvania pôsobí v každom okamžiku na všetky spiny vo vzorke rovnako, kým impulzy Bi(t) generované tepelným pohybom molekúl sú náhodné v čase i mikroskopickej lokalite svojho pôsobenia. Ako je to je ilustrované na obrázku 13 hustota pohybov Bi(t) na rezonancii spinov je maximálna ak tepelný pohyb vo vzorke je charakterizovaný korelačným časom τc = 1/ω0. Pre spiny s rezonančnou frekvenciou ω0~500 MHz je to korelačný čas τc~0.32ns.
Príspevok náhodných polí s frekvenciou blízkou nule (ω/ω0~0) k relaxácií spinov súvisí s efektom nehomogenít poľa Bo na stratu fázovej koherencie spinov. Okrem vlastnej nehomogenity poľa ΔBo (danou nedokonalým naladením cievok vytvárajúcich pole Bo ), ktorá sa s časom nemení a ktorej efekt sa dá eliminovať (spinové echo; pozri neskôr) k časovo premenlivej nehomogenite poľa ΔBo(t) prispievajú aj náhodné lokálne polia Bi,z(t) orientované v smere osi z s frekvenciou blízkou nule (pri náhodných poliach s vyššou frekvenciou sa ich efekt rýchlo spriemeruje na nulu: kladné a záporné odchýlky sa vzájomne vykompenzujú). Tieto polia spôsobujú zmenu orientácie Mx a My zložiek magnetizácie. Rôzna úroveň výsledného poľa Bo(t)= Bo+ΔBo+Bi,z(t) v rôznych lokalitách vzorky znamená rozdiely v rýchlosti precesie spinov v týchto lokalitách a následne postupnú zmenu ich relatívnej orientácie spinov v rovine xy. Ak vo vzorke bola predtým vytvorená nejaká fázová koherencia (napr. Mxy), tento mechanizmus spôsobuje jej postupný zánik (relaxáciu). Nehomogenity Bi,z(t) ako aj ΔBo majú pritom zanedbateľný efekt na Mz zložku magnetizácie. Na rozdiel od efektu vlastnej nehomogenity ΔBo je efekt náhodných poli Bi,z(t) na Mxy zložku magnetizácie nezvratný.
Najčastejším druhom pohybu s frekvenciou v oblasti Larmorovej frekvencie spinov pri bežných vzorkách z organickej chémie a biochémie je rotačný pohyb molekúl. Korelačný čas τc v tomto prípade znamená štatisticky priemerný čas za ktorý sa molekula pootočí o jeden radián.
Korelačný čas τc závisí od veľkosti, tvaru molekuly, miesta lokalizácie spinov v molekule ako aj viskozity vzorky. Často sa však jeho približný odhad robí na základe veľkosti molekúl. Za stredné veľké molekuly sa v organickej chémii považujú molekuly z molekulovou hmotnosťou okolo 1000. Ich rotačný korelačný čas je rádovo desatiny nanosekúnd (~10-10 s). U malých makromolekúl (~5kDaltonov) je to niekoľko nanosekúnd (~10-9s); u veľkých desiatky až stovky nanosekúnd (~10-8– 10-7s). Naopak malé organické molekuly v malo viskóznych roztokoch majú korelačný čas rádovo pikosekundy až desiatky pikosekúnd (~10-12 -10-11s).
Frekvencia zodpovedajúca korelačnému času náhodného pohybu stredne veľkých molekúl (ω = 1/τc) je v oblasti precesie 1H jadier pri ich umiestnení v bežne dostupných NMR magnetoch (stovky MHz). Znamená to, že hustota náhodných pohybov je pre stredné veľké molekuly v blízkosti jej optimálnej hodnoty (1/τc~ ω0). Inými slovami relaxácia Mz zložky magnetizácie v prípade stredne veľkých molekúl bude rýchlejšia ako v prípade veľkých i malých molekúl. Je to zaujímavý fenomén ktorý súvisí s charakterom náhodných rotačných pohybov.
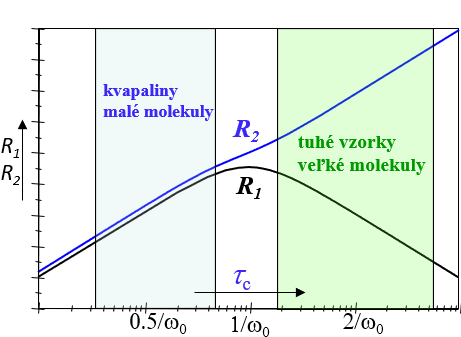
Na základe predchádzajúcich úvah možno si vytvoriť intuitívnu predstavu a závislosti relaxačných časov od pohyblivosti spinov ako je to ukázané na obr. 13a. Rýchlosť relaxácie Mz bude mať maximálnu hodnotu pre stredné veľké molekuly (τc∿1/ω0 ) pretože majú najväčšiu hustotu náhodných pohybov v oblasti svojej rezonančnej frekvencie ω0. Väčšie (τc>1/ω0 ) i menšie (τc<1/ω0 ) molekuly budú mať hustotu ich náhodných pohybov v oblasti ω0 menšiu a preto rýchlosť ich Mz relaxácie bude pomalšia. Čím sa ich pohyblivosť bude viac líšiť od pohyblivosti stredne veľkých molekúl tým pomalšia bude ich Mz relaxácia.
Mxy zložka magnetizácie vykazuje rozdielnu závislosť od pohyblivosti molekúl. Je to dôsledok toho, že k jej relaxácií prispievajú okrem náhodných poli na rezonančnej frekvencií aj náhodné polia z oblasti veľmi malých frekvencií. Pre malé organické molekuly je tento príspevok malý a preto rýchlosť relaxácie Mxy je pre tieto molekuly podobná rýchlosti relaxácie Mz. Pre veľké molekuly je však tento príspevok významný (až dominantný ), a preto rýchlosť relaxácie Mxy monotónne rastie s veľkosťou molekúl.
Vo všetkých predchádzajúcich úvahách o relaxácií spinov sa implicitne predpokladalo, že pohyb spinov je určený iba náhodným pohybom molekúl. Avšak rôzne spiny viazané v tej istej molekule pociťujú náhodné polia s rovnakou frekvenčnou distribúciou ako celá molekula len v prípade rigidných, sféricky symetrických molekúl. Pre nesymetrické molekuly a molekuly, ktorých fragmenty vykazujú rôznu pohyblivosť je popis náhodných procesov ovplyvňujúcich ich relaxáciu zložitejší a čitateľ si ho môže nájsť v literatúre [1-3].
Rozdiely v lokálnej pohyblivosti sa často dajú jednoducho odhadnúť zo štruktúry molekuly. Tieto rozdiely sa potom predvídateľným spôsobom prejavia na rýchlosti relaxácie relevantných spinov, čo sa dá využiť pri praktickej analýze NMR dát (pozri nižšie).
[1a] Lipari, G., & Szabo, A. (1982). Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 1. Theory and range of validity. Journal of the American Chemical Society, 104(17), 4546–4559. doi:10.1021/ja00381a009.
[1b] Lipari, G., & Szabo, A. (1982). Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 2. Analysis of experimental results. Journal of the American Chemical Society, 104(17), 4559–4570. doi:10.1021/ja00381a010
[2] Redfield, A. G. (2007). Relaxation Theory: Density Matrix Formulation. Encyclopedia of Magnetic Resonance. doi:10.1002/9780470034590.emrstm0463
[3] Wangsness, R. K., & Bloch, F. (1953). The Dynamical Theory of Nuclear Induction. Physical Review, 89(4), 728–739. doi:10.1103/physrev.89.728







